Boolean - Boolean Definition & Meaning
Recent Posts
- Ha bee ice cream
- Doctor2u
- Bkss 6.0 semakan 2021
- Mc vs
- Alight motion apk 4.0.4
- Raditya oloan
- Bintai kinden share price
- Kemaskini bantuan bkm 2022
- Progress in malay
- Cikgu selalu memarahi saya
- Contoh email english
- Sony ericsson k750i
- Massage near me
- Contoh resume
- Semakan bkss sarawak 2022
- Tickethotline piala malaysia
- The frog prince thai dramacool
Boolean
Boolean Searching
Boolean Definition & Meaning
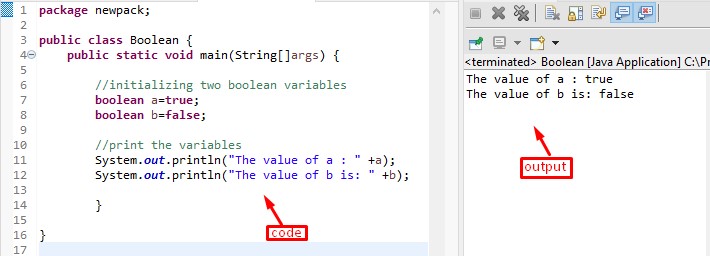
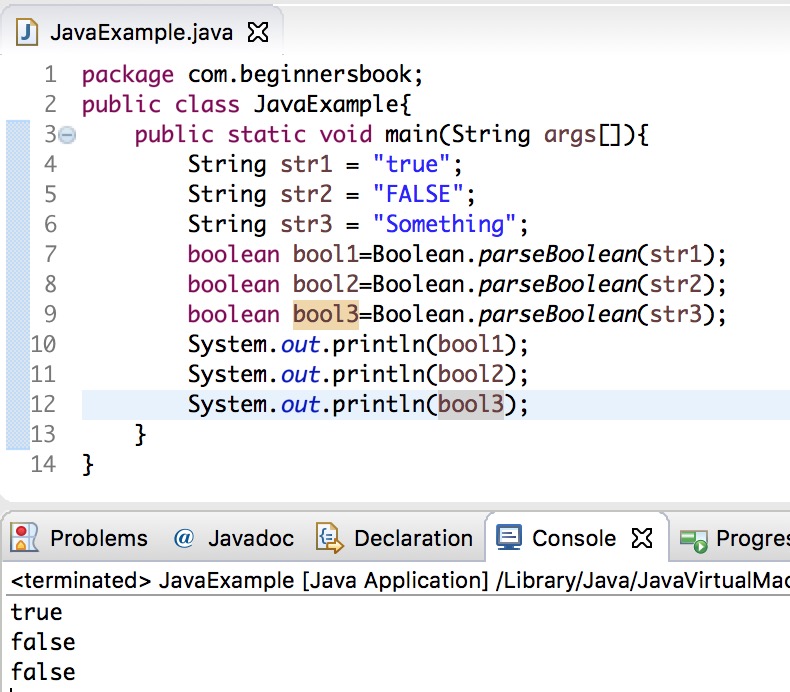
Java Boolean
However, if we represent each divisor of n by the set of its prime factors, we find that this nonconcrete Boolean algebra is to the concrete Boolean algebra consisting of all sets of prime factors of n, with union corresponding to least common multiple, intersection to greatest common divisor, and complement to division into n.
.
Again the answer is yes.
Boolean Struct (System)
This example is an instance of the following notion.
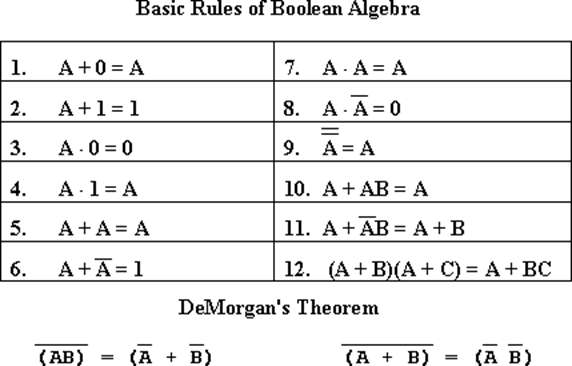
These semantics permit a translation between tautologies of propositional logic and equational theorems of Boolean algebra.
Otherwise, the result is false.
- Related articles
2022 blog.dabchy.com